產品分類

山東合運電氣有限公司
手機:15588886921(同微信)
官網:www.ldrcw.com.cn
郵箱:2466458158@qq.com
電勢
時間:2022-10-16 人氣: 來源:山東合運電氣有限公司
在這篇文章內,向量與標量分別用粗體與斜體顯示。例如,位置向量通常用{\displaystyle\mathbf{r}\,\!}\mathbf{r}\,\!表示;而其大小則用{\displaystyle r\,\!}r\,\!來表示。
在靜電學里,電勢(electric potential)又稱電位[1],是描述電場中某一點之能量高低性質的物理標量,操作型定義為“電場中某處的電勢”等于“處于電場中該位置的單位電荷所具有的電勢能”[2],單位用伏特。
電勢的數值不具有絕對意義,只具有相對意義,因此為了便于分析問題,必須設定一個參考位置,并把它設為零,稱為零勢能點。通常,會把無窮遠處的電勢設定為零。那么,電勢可以定義如下:假設檢驗電荷從無窮遠位置,經過任意路徑,克服電場力,以緩慢、沒有產生加速度的方式移動到某位置,則在這位置的電勢,等于因移動檢驗電荷所做的功與檢驗電荷的電荷量的比值。在國際單位制里,電勢的單位為伏特({\displaystyle\scriptstyle{{\text{V}}={\text{J}}/{\text{C}}}}{\displaystyle\scriptstyle{{\text{V}}={\text{J}}/{\text{C}}}})(Volt),它是為了紀念意大利物理學家亞歷山德羅·伏打(Alessandro Volta)而命名。
電勢必需滿足泊松方程,同時符合相關邊界條件;假設在某區域內的電荷密度為零,則泊松方程約化為拉普拉斯方程,電勢必需滿足拉普拉斯方程。
在電動力學里,當含時電磁場存在的時候,電勢可以延伸為“廣義電勢”。特別注意,廣義電勢不能被視為電勢能每單位電荷。
簡介
處于外電場的帶電粒子會受到外電場施加的作用力,稱為電場力,促使帶電粒子加速運動。對于帶正電粒子,電場力與電場同方向;對于帶負電粒子,電場力與電場反方向。電場力的數值大小與電荷量、電場數值大小成正比。
作用力與勢能之間有非常直接的關系。隨著物體朝著作用力的方向的加速運動,物體的動能變大,勢能變小。例如,一個石頭在山頂的重力勢能大于在山腳的重力勢能。隨著物體的滾落,重力勢能變小,動能變大。
對于某種特別作用力,科學家可以定義其向量場和其位勢,使得物體因為這向量場而具有的勢能,只與物體位置、參考位置之間的距離有關。稱這種作用力為保守力,這種向量場為保守場。
例如,重力、靜電場的電場力,都是保守力。靜電場的標勢稱為電勢,或稱為靜電勢。
電勢和磁矢勢共同形成一個四維向量,稱為四維勢。從某一個慣性參考系觀察到的四維勢,應用洛倫茲變換,可以計算出另外一個慣性參考系所觀察到的四維勢。
靜電學里的電勢
在靜電學里,電場{\displaystyle\mathbf{E}}\mathbf{E}內某位置{\displaystyle\mathbf{r}}\mathbf{r}的電勢{\displaystyle\phi}\phi,以方程定義為[2]
{\displaystyle\phi(\mathbf{r})\{\stackrel{def}{=}}\U_{\mathrm{E}}(\mathbf{r})/q}\phi(\mathbf{r})\\stackrel{def}{=}\U_\mathrm{E}(\mathbf{r})/q;
其中,{\displaystyle U_{\mathrm{E}}}U_\mathrm{E}是在位置{\displaystyle\mathbf{r}}\mathbf{r}的檢驗電荷{\displaystyle q}q所具有的電勢能。
電勢能的數值是人為設定的,沒有絕對意義,只有相對于某參考位置的已設定參考值時才有物理意義。假若要設定電勢能在空間任意位置的數值,必須先設定其在某參考位置{\displaystyle\mathbf{r}_{0}}\mathbf{r}_0的數值。為了方便運算,假設其參考數值為0。然后,就可以將在位置{\displaystyle\mathbf{r}}\mathbf{r}的電勢能{\displaystyle U_{\mathrm{E}}(\mathbf{r})}U_\mathrm{E}(\mathbf{r})定義為從參考位置{\displaystyle\mathbf{r}_{0}}\mathbf{r}_0緩慢地將檢驗電荷{\displaystyle q}q移動至{\displaystyle\mathbf{r}}\mathbf{r}所需做的機械功{\displaystyle W}W:
{\displaystyle U_{\mathrm{E}}(\mathbf{r})\{\stackrel{def}{=}}\W}U_\mathrm{E}(\mathbf{r})\\stackrel{def}{=}\W。
移動檢驗電荷時所施加的外力{\displaystyle\mathbf{F}}\mathbf{F},必須恰巧抵消處于電場{\displaystyle\mathbf{E}}\mathbf{E}的檢驗電荷{\displaystyle q}q所感受到的電場力{\displaystyle q\mathbf{E}}q\mathbf{E},即{\displaystyle\mathbf{F}=-q\mathbf{E}}\mathbf{F}=-q\mathbf{E}。其所做機械功等于外力{\displaystyle\mathbf{F}}\mathbf{F}的路徑積分:
{\displaystyle W=\int _{\mathbb{L}}\mathbf{F}\cdot\mathrmkmk00wm{\boldsymbol{\ell}}=-q\int _{\mathbb{L}}\mathbf{E}\cdot\mathrmkmk00wm{\boldsymbol{\ell}}}W=\int_\mathbb{L}\mathbf{F}\cdot\mathrmkmk00wm\boldsymbol{\ell}=-q\int_\mathbb{L}\mathbf{E}\cdot\mathrmkmk00wm\boldsymbol{\ell};
其中,{\displaystyle\mathbb{L}}\mathbb{L}是從參考位置{\displaystyle\mathbf{r}_{0}}\mathbf{r}_0到位置{\displaystyle\mathbf{r}}\mathbf{r}的一條任意路徑,{\displaystyle\mathrmkmk00wm{\boldsymbol{\ell}}}\mathrmkmk00wm{\boldsymbol{\ell}}是微小線元素。
在靜電學里,{\displaystyle\mathbf{\nabla}\times\mathbf{E}=0}\mathbf{\nabla}\times\mathbf{E}=0,電場是保守場,所以,在積分時,可以選擇任意路徑{\displaystyle\mathbb{L}}\mathbb{L},計算出來的結果都一樣。欲知更詳盡細節,請參閱條目保守力。由于這方程右邊的路徑積分跟路徑{\displaystyle\mathbb{L}}\mathbb{L}無關,只跟路徑的初始位置{\displaystyle\mathbf{r}_{0}}\mathbf{r}_0、終止位置{\displaystyle\mathbf{r}}\mathbf{r}有關,因此若能夠假設無窮遠位置{\displaystyle\infty}\infty的電勢能為0,則可以設定參考位置{\displaystyle\mathbf{r}_{0}}\mathbf{r}_0在無窮遠位置{\displaystyle\infty}\infty:
{\displaystyle U_{\mathrm{E}}(\mathbf{r})=-q\int _{\infty}^{\mathbf{r}}\mathbf{E}\cdot\mathrmkmk00wm{\boldsymbol{\ell}}}U_\mathrm{E}(\mathbf{r})=-q\int_\infty^\mathbf{r}\mathbf{E}\cdot\mathrmkmk00wm\boldsymbol{\ell}。
所以,電勢就是從無窮遠位置到檢驗位置對于電場做路徑積分所得結果的負值:
{\displaystyle\phi(\mathbf{r})=-\int _{\infty}^{\mathbf{r}}\mathbf{E}\cdot\mathrmkmk00wm{\boldsymbol{\ell}}}\phi(\mathbf{r})=-\int_\infty^\mathbf{r}\mathbf{E}\cdot\mathrmkmk00wm\boldsymbol{\ell}。
在任意兩個位置{\displaystyle\mathbf{r}_{1}}\mathbf{r}_1、{\displaystyle\mathbf{r}_{2}}\mathbf{r}_2之間的“電勢差”{\displaystyle\Delta\phi}\Delta\phi為
{\displaystyle\Delta\phi=\phi(\mathbf{r}_{2})-\phi(\mathbf{r}_{1})=-\int _{\mathbf{r}_{1}}^{\mathbf{r}_{2}}\mathbf{E}\cdot\mathrmkmk00wm{\boldsymbol{\ell}}}\Delta\phi=\phi(\mathbf{r}_2)-\phi(\mathbf{r}_1)=-\int_{\mathbf{r}_1}^{\mathbf{r}_2}\mathbf{E}\cdot\mathrmkmk00wm\boldsymbol{\ell}。
由于電場{\displaystyle\mathbf{E}}\mathbf{E}是保守場,電勢差也與積分路徑無關,只跟積分路徑的初始位置與終止位置有關。
點電荷
由點電荷Q所產生的電勢,在距離r時,可表示為
{\displaystyle V={\frac{1}{4\pi\varepsilon _{0}}}{\frac{Q}{r}}}V=\frac{1}{4\pi\varepsilon_0}\frac{Q}{r}
其中,ε0是真空電容率。
在無限遠處,電勢為零。由多個點電荷產生的電勢,相等于各點電荷所產生的電勢之和。此外,電勢場是標量場,電場則是向量場。
疊加原理
電場遵守疊加原理:假設在三維空間里,由兩組完全不相交的電荷分布所產生的電場分別為{\displaystyle\mathbf{E}_{1}}\mathbf{E}_1、{\displaystyle\mathbf{E}_{2}}\mathbf{E}_2,則總電場為{\displaystyle\mathbf{E}_{t}=\mathbf{E}_{1}+\mathbf{E}_{2}}\mathbf{E}_t=\mathbf{E}_1+\mathbf{E}_2。
總電勢為每單位電荷克服電場力所做的機械功之和:
{\displaystyle\phi _{t}(\mathbf{r})=-\int _{\infty}^{\mathbf{r}}\mathbf{E}_{t}\cdot\mathrmkmk00wm{\boldsymbol{\ell}}=-\int _{\infty}^{\mathbf{r}}(\mathbf{E}_{1}+\mathbf{E}_{2})\cdot\mathrmkmk00wm{\boldsymbol{\ell}}=\phi _{1}(\mathbf{r})+\phi _{2}(\mathbf{r})}\phi_t(\mathbf{r})=-\int_\infty^\mathbf{r}\mathbf{E}_t\cdot\mathrmkmk00wm\boldsymbol{\ell}=-\int_\infty^\mathbf{r}(\mathbf{E}_1+\mathbf{E}_2)\cdot\mathrmkmk00wm\boldsymbol{\ell}=\phi_1(\mathbf{r})+\phi_2(\mathbf{r})。
所以,電勢也遵守疊加原理。當計算一組電荷分布所產生的電勢時,只需要知道在電荷分布的每個源位置的單獨電荷所產生在檢驗位置的電勢,就可以應用積分運算,得到整個電荷分布所產生在檢驗位置的電勢。
電勢的微分方程
應用積分符號內取微分方法,電勢的梯度為
{\displaystyle\mathbf{\nabla}\phi(\mathbf{r})=-\mathbf{\nabla}\int _{\infty}^{\mathbf{r}}\mathbf{E}(\mathbf{r}')\cdot\mathrmkmk00wm{\boldsymbol{\ell}}^{\,\prime}=-\mathbf{E}(\mathbf{r})}\mathbf{\nabla}\phi(\mathbf{r})=-\mathbf{\nabla}\int_\infty^\mathbf{r}\mathbf{E}(\mathbf{r}')\cdot\mathrmkmk00wm\boldsymbol{\ell}^{\,\prime}=-\mathbf{E}(\mathbf{r})。
所以,電場與電勢之間的關系為
{\displaystyle\mathbf{E}(\mathbf{r})=-\mathbf{\nabla}\phi(\mathbf{r})}\mathbf{E}(\mathbf{r})=-\mathbf{\nabla}\phi(\mathbf{r})。
根據高斯定律的方程,
{\displaystyle\mathbf{\nabla}\cdot\mathbf{E}=\rho/\epsilon _{0}}\mathbf{\nabla}\cdot\mathbf{E}=\rho/\epsilon_0;
其中,{\displaystyle\rho}\rho是電荷密度,{\displaystyle\epsilon _{0}}\epsilon _{0}是電常數。
所以,電勢滿足泊松方程:
{\displaystyle\nabla^{2}\phi=-\rho/\epsilon _{0}}\nabla^2\phi=-\rho/\epsilon_0。
假設電荷密度為零,則這方程變為拉普拉斯方程:
{\displaystyle\nabla^{2}\phi=0}\nabla^2\phi=0。
請注意,假若{\displaystyle\mathbf{\nabla}\times\mathbf{E}\neq 0}\mathbf{\nabla}\times\mathbf{E}\ne 0,也就是說,電場不具保守性(由于隨時間變化的磁場造成的效應;參閱麥克斯韋方程組),則不能使用這些方程。
由于電勢乃是標量,而電場是具有三個分量的向量,所以,很多時候,使用電勢來解析問題會省去很多運算工作,帶來很大的便利。
拉普拉斯方程的解答
在某空間區域內,假設電荷密度為零,則電勢必須滿足拉普拉斯方程,并且符合所有相關邊界條件。
邊界條件
在靜電學里,有三種邊界條件:
狄利克雷邊界條件:在所有邊界,電勢都已良態給定。具有這種邊界條件的問題稱為狄利克雷問題。
紐曼邊界條件:在所有邊界,電勢的法向導數都已良態給定。具有這種邊界條件的問題稱為紐曼問題。
混合邊界條件:一部分邊界的電勢都已良態給定,其它邊界的電勢的法向導數也已良態給定。
根據拉普拉斯方程的唯一性定理,對于這些種類的邊界條件,拉普拉斯方程的解答都具有唯一性。所以,只要找到一個符合邊界條件的解答,則這解答必定為正確解答。
分離變數法
應用分離變數法來解析拉普拉斯方程,可以將問題的偏微分方程改變為一組較容易解析的常微分方程。對于一般問題,通常會采用直角坐標系、圓柱坐標系或球坐標系來分離拉普拉斯方程。但是,對于其它比較特別的問題,另外還有八種坐標系可以用來分離拉普拉斯方程。[3]分離之后,找到每一個常微分方程的通解(通常為一組本征方程的疊加),電勢可以表達為這些通解的乘積。將這表達式與邊界條件相匹配,就可以設定一般解的系數,從而找到問題的特解。根據拉普拉斯方程的唯一性定理,這特解也是唯一的正確解答。
兩個半平面導體案例
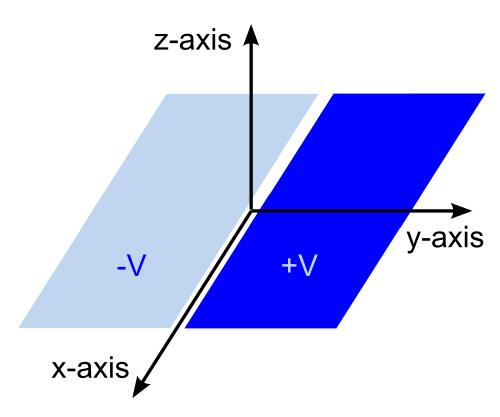
被位于{\displaystyle y=0}y=0的絕緣線條分隔為處于y+、y--半平面的兩個導體的電勢分別設定為{\displaystyle+V}+V、{\displaystyle-V}-V。
假設在xy-平面的無限平面導體被一條位于{\displaystyle y=0}y=0的絕緣線條分為兩半,兩個處于y+、y--半平面的導體的電勢分別設定為{\displaystyle+V}+V、{\displaystyle-V}-V,則計算z+-半空間任意位置的電勢這問題,由于邊界條件的幾何形狀適合用直角坐標來描述,可以以直角坐標{\displaystyle(x,y,z)}(x,y,z)將拉普拉斯方程表示為:
{\displaystyle\nabla^{2}\phi={\frac{\partial^{2}\phi}{\partial x^{2}}}+{\frac{\partial^{2}\phi}{\partial y^{2}}}+{\frac{\partial^{2}\phi}{\partial z^{2}}}=0}\nabla^2\phi=\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}+\frac{\partial^2\phi}{\partial z^2}=0。
因為這案例與x-坐標無關,方程可以簡化為
{\displaystyle\nabla^{2}\phi(y,z)={\frac{\partial^{2}\phi}{\partial y^{2}}}+{\frac{\partial^{2}\phi}{\partial z^{2}}}=0}\nabla^2\phi(y,z)=\frac{\partial^2\phi}{\partial y^2}+\frac{\partial^2\phi}{\partial z^2}=0。
應用分離變數法,猜想解答的形式為
{\displaystyle\phi(y,z)=Y(y)Z(z)}\phi(y,z)=Y(y)Z(z)。
將這公式代入拉普拉斯方程,則可得到
{\displaystyle{\frac{1}{Y(y)}}\{\frac{\mathrmkmk00wm^{2}Y(y)}{\mathrmkmk00wmy^{2}}}+{\frac{1}{Z(z)}}\{\frac{\mathrmkmk00wm^{2}Z(z)}{\mathrmkmk00wmz^{2}}}=0}\frac{1}{Y(y)}\\frac{\mathrmkmk00wm^2 Y(y)}{\mathrmkmk00wmy^2}+\frac{1}{Z(z)}\\frac{\mathrmkmk00wm^2 Z(z)}{\mathrmkmk00wmz^2}=0。
注意到這方程的每一個項目都只含有一個變量,并且跟其它變量無關。所以,每一個項目都等于常數:
{\displaystyle{\frac{1}{Y(y)}}\{\frac{\mathrmkmk00wm^{2}Y(y)}{\mathrmkmk00wmy^{2}}}=C}\frac{1}{Y(y)}\\frac{\mathrmkmk00wm^2 Y(y)}{\mathrmkmk00wmy^2}=C、
{\displaystyle{\frac{1}{Z(z)}}\{\frac{\mathrmkmk00wm^{2}Z(z)}{\mathrmkmk00wmz^{2}}}=-C}\frac{1}{Z(z)}\\frac{\mathrmkmk00wm^2 Z(z)}{\mathrmkmk00wmz^2}=-C。
這樣,一個二次偏微分方程被改變為兩個簡單的二次常微分方程。解答分別為
{\displaystyle Y(y)=A_{1}e^{iky}+A_{2}e^{-iky}}Y(y)=A_1 e^{iky}+A_2 e^{-iky}、
{\displaystyle Z(z)=B_{1}e^{kz}+B_{2}e^{-kz}}Z(z)=B_1 e^{kz}+B_2 e^{-kz};
其中,{\displaystyle A_{1}(k)}A_1(k)、{\displaystyle A_{2}(k)}A_2(k)、{\displaystyle B_{1}(k)}B_1(k)、{\displaystyle B_{2}(k)}B_2(k)都是系數函數。
當{\displaystyle z}z趨向于無窮大時,{\displaystyle Z(z)}Z(z)趨向于零,所以,{\displaystyle B_{1}=0}B_1=0。綜合起來,電勢為
{\displaystyle\phi(y,z)=\int _{0}^{\infty}(A_{1}e^{iky}+A_{2}e^{-iky})e^{-kz}\mathrmkmk00wmk}\phi(y,z)=\int_0^{\infty}(A_1 e^{iky}+A_2 e^{-iky})e^{-kz}\mathrmkmk00wmk。
由于在{\displaystyle z=0}z=0,y+、y--半平面的電勢分別為{\displaystyle+V}+V、{\displaystyle-V}-V,所以,
當{\displaystyle y>0}y>0時,{\displaystyle\int _{0}^{\infty}(A_{1}e^{iky}+A_{2}e^{-iky})\mathrmkmk00wmk=+V}\int_0^{\infty}(A_1 e^{iky}+A_2 e^{-iky})\mathrmkmk00wmk=+V、
當{\displaystyle y<0}y<0時,{\displaystyle\int _{0}^{\infty}(A_{1}e^{iky}+A_{2}e^{-iky})\mathrmkmk00wmk=-V}\int_0^{\infty}(A_1 e^{iky}+A_2 e^{-iky})\mathrmkmk00wmk=-V。
應用傅里葉變換,可以得到
{\displaystyle A_{1}(k)={\frac{V}{2\pi}}\left(\int _{0}^{\infty}e^{-iky'}\mathrmkmk00wmy'-\int _{-\infty}^{0}e^{-iky'}\mathrmkmk00wmy'\right)}A_1(k)=\frac{V}{2\pi}\left(\int_0^{\infty}e^{-iky'}\mathrmkmk00wmy'-\int_{-\infty}^0 e^{-iky'}\mathrmkmk00wmy'\right)、
{\displaystyle A_{2}(k)={\frac{V}{2\pi}}\left(\int _{0}^{\infty}e^{iky'}\mathrmkmk00wmy'-\int _{-\infty}^{0}e^{iky'}\mathrmkmk00wmy'\right)}A_2(k)=\frac{V}{2\pi}\left(\int_0^{\infty}e^{iky'}\mathrmkmk00wmy'-\int_{-\infty}^0 e^{iky'}\mathrmkmk00wmy'\right)。
所以,由{\displaystyle A_{1}(k)}A_1(k)項目貢獻出的電勢為
{\displaystyle{\begin{aligned}\phi _{1}&={\frac{V}{2\pi}}\int _{0}^{\infty}\mathrmkmk00wmk\left\{\int _{0}^{\infty}e^{ik(y-y')-kz}\mathrmkmk00wmy'-\int _{-\infty}^{0}e^{ik(y-y')-kz}\mathrmkmk00wmy'\right\}\\&=-\{\frac{V}{2\pi}}\int _{0}^{\infty}{\frac{\mathrmkmk00wmy'}{i(y-y')-z}}+\{\frac{V}{2\pi}}\int _{-\infty}^{0}{\frac{\mathrmkmk00wmy'}{i(y-y')-z}}\\\end{aligned}}}\begin{align}\phi_1&=\frac{V}{2\pi}\int_0^{\infty}\mathrmkmk00wmk\left\{\int_0^{\infty}e^{ik(y-y')-kz}\mathrmkmk00wmy'-\int_{-\infty}^0e^{ik(y-y')-kz}\mathrmkmk00wmy'\right\}\\
&=-\\frac{V}{2\pi}\int_0^{\infty}\frac{\mathrmkmk00wmy'}{i(y-y')-z}+\\frac{V}{2\pi}\int_{-\infty}^0\frac{\mathrmkmk00wmy'}{i(y-y')-z}\\
\end{align}。
類似地,由{\displaystyle A_{2}(k)}A_2(k)項目貢獻出的電勢為
{\displaystyle{\begin{aligned}\phi _{2}&={\frac{V}{2\pi}}\int _{0}^{\infty}\mathrmkmk00wmk\left\{\int _{0}^{\infty}e^{-ik(y-y')-kz}\mathrmkmk00wmy'-\int _{-\infty}^{0}e^{-ik(y-y')-kz}\mathrmkmk00wmy'\right\}\\&=-\{\frac{V}{2\pi}}\int _{0}^{\infty}{\frac{\mathrmkmk00wmy'}{-i(y-y')-z}}+\{\frac{V}{2\pi}}\int _{-\infty}^{0}{\frac{\mathrmkmk00wmy'}{-i(y-y')-z}}\\\end{aligned}}}\begin{align}\phi_2&=\frac{V}{2\pi}\int_0^{\infty}\mathrmkmk00wmk\left\{\int_0^{\infty}e^{-ik(y-y')-kz}\mathrmkmk00wmy'-\int_{-\infty}^0e^{-ik(y-y')-kz}\mathrmkmk00wmy'\right\}\\
&=-\\frac{V}{2\pi}\int_0^{\infty}\frac{\mathrmkmk00wmy'}{-i(y-y')-z}+\\frac{V}{2\pi}\int_{-\infty}^0\frac{\mathrmkmk00wmy'}{-i(y-y')-z}\\
\end{align}。
總電勢為[4]
{\displaystyle{\begin{aligned}\phi&={\frac{Vz}{\pi}}\int _{0}^{\infty}{\frac{\mathrmkmk00wmy'}{(y-y')^{2}+z^{2}}}-\{\frac{Vz}{\pi}}\int _{-\infty}^{0}{\frac{\mathrmkmk00wmy'}{(y-y')^{2}+z^{2}}}\\&={\frac{2V}{\pi}}\\arctan{\left({\frac{y}{z}}\right)}\\\end{aligned}}}\begin{align}\phi&=\frac{Vz}{\pi}\int_0^{\infty}\frac{\mathrmkmk00wmy'}{(y-y')^2+z^2}-\\frac{Vz}{\pi}\int_{-\infty}^0\frac{\mathrmkmk00wmy'}{(y-y')^2+z^2}\\
&=\frac{2V}{\pi}\\arctan{\left(\frac{y}{z}\right)}\\
\end{align}。
泊松方程的解答
電荷分布所產生的電勢
根據庫侖定律,一個源位置為{\displaystyle\mathbf{r}'}\mathbf{r}'的點電荷{\displaystyle q}q,所產生在任意位置{\displaystyle\mathbf{r}}\mathbf{r}的電場為
{\displaystyle\mathbf{E}(\mathbf{r})={\frac{q}{4\pi\epsilon _{0}}}\{\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^{3}}}}\mathbf{E}(\mathbf{r})=\frac{q}{4\pi\epsilon_0}\\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}。
對于一群點電荷,應用疊加原理,總電場等于每一個點電荷所產生的電場的疊加。體積區域{\displaystyle\mathbb{V}'}\mathbb{V}'內部電荷密度為{\displaystyle\rho(\mathbf{r}')}\rho(\mathbf{r}')的電荷分布,在檢驗位置{\displaystyle\mathbf{r}}\mathbf{r}所產生的電場為
{\displaystyle\mathbf{E}(\mathbf{r})={\frac{1}{4\pi\epsilon _{0}}}\int _{\mathbb{V}'}\rho(\mathbf{r}'){\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^{3}}}\\mathrmkmk00wm^{3}r'}\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\epsilon_0}\int_{\mathbb{V}'}\rho(\mathbf{r}')\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\\mathrmkmk00wm^3 r';
其中,{\displaystyle\mathrmkmk00wm^{3}r'}\mathrmkmk00wm^3 r'是微小體積元素。
應用一條向量恒等式,
{\displaystyle\nabla{\frac{1}{|\mathbf{r}-\mathbf{r}'|}}=-\{\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^{3}}}}\nabla\frac{1}{|\mathbf{r}-\mathbf{r}'|}=-\\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3},
可以得到
{\displaystyle\mathbf{E}(\mathbf{r})=-\{\frac{1}{4\pi\epsilon _{0}}}\nabla\int _{\mathbb{V}'}{\frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}}\\mathrmkmk00wm^{3}r'}\mathbf{E}(\mathbf{r})=-\\frac{1}{4\pi\epsilon_0}\nabla\int_{\mathbb{V}'}\frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\\mathrmkmk00wm^3 r'。
設定在無窮遠的電勢為參考值0,則在任意位置的電勢為
{\displaystyle\phi(\mathbf{r})={\frac{1}{4\pi\epsilon _{0}}}\int _{\mathbb{V}'}{\frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}}\\mathrmkmk00wm^{3}r'}\phi(\mathbf{r})=\frac{1}{4\pi\epsilon_0}\int_{\mathbb{V}'}\frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\\mathrmkmk00wm^3 r';(1)
應用一則關于狄拉克δ函數的向量恒等式
{\displaystyle\nabla^{2}\left({\frac{1}{|\mathbf{r}-\mathbf{r}'|}}\right)=-4\pi\delta(\mathbf{r}-\mathbf{r}')}\nabla^2\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right)
=-4\pi\delta(\mathbf{r}-\mathbf{r}'),
假設檢驗位置{\displaystyle\mathbf{r}}\mathbf{r}在積分體積{\displaystyle\mathbb{V}'}\mathbb{V}'內,則可得到泊松方程:
{\displaystyle\nabla^{2}\phi(\mathbf{r})={\frac{1}{4\pi\epsilon _{0}}}\int _{\mathbb{V}'}\nabla^{2}\left({\frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}}\right)\\mathrmkmk00wm^{3}r'=-\{\frac{1}{\epsilon _{0}}}\int _{\mathbb{V}'}\rho(\mathbf{r}')\delta(\mathbf{r}-\mathbf{r}')\\mathrmkmk00wm^{3}r'=-\{\frac{\rho(\mathbf{r})}{\epsilon _{0}}}}\nabla^2\phi(\mathbf{r})=\frac{1}{4\pi\epsilon_0}\int_{\mathbb{V}'}\nabla^2\left(\frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\right)
\\mathrmkmk00wm^3 r'=-\\frac{1}{\epsilon_0}\int_{\mathbb{V}'}\rho(\mathbf{r}')\delta(\mathbf{r}-\mathbf{r}')\\mathrmkmk00wm^3 r'
=-\\frac{\rho(\mathbf{r})}{\epsilon_0}。
所以,電勢的方程(1)為泊松方程的解答。
邊界條件
電勢的方程(1)只考慮到一群電荷分布所產生的電勢。假若遭遇邊界條件為電勢的靜電學問題,就不能使用方程(1),必需使用更具功能的方法。
根據格林第二恒等式,對于任意良態函數{\displaystyle\phi(\mathbf{r})}\phi(\mathbf{r})與{\displaystyle\psi(\mathbf{r})}\psi(\mathbf{r}),[5]
{\displaystyle\int _{\mathbb{V}}\left(\phi\nabla^{2}\psi-\psi\nabla^{2}\phi\right)\\mathrmkmk00wm^{3}r=\oint _{\mathbb{S}}\left(\phi{\partial\psi\over\partial n}-\psi{\partial\phi\over\partial n}\right)\\mathrmkmk00wm^{2}r}\int_{\mathbb{V}}\left(\phi\nabla^2\psi-\psi\nabla^2\phi\right)\\mathrmkmk00wm^3 r=\oint_{\mathbb{S}}\left(\phi{\partial\psi\over\partial n}-\psi{\partial\phi\over\partial n}\right)\\mathrmkmk00wm^2 r;
其中,{\displaystyle\mathbb{V}}\mathbb{V}是積分體積,{\displaystyle\mathbb{S}}\mathbb{S}是包住{\displaystyle\mathbb{V}}\mathbb{V}的閉表面,{\displaystyle\mathrmkmk00wm^{2}r}\mathrmkmk00wm^2 r是微小面元素,{\displaystyle\partial\phi\over\partial n}\partial\phi\over\partial n或{\displaystyle\partial\phi\over\partial n}\partial\phi\over\partial n都是取垂直于閉表面{\displaystyle\mathbb{S}}\mathbb{S}的法向導數,都是從積分體積{\displaystyle\mathbb{V}}\mathbb{V}朝外指出。
設定{\displaystyle\phi(\mathbf{r}')}\phi(\mathbf{r}')為在{\displaystyle\mathbf{r}'}\mathbf{r}'的電勢,{\displaystyle\psi={\frac{1}{|\mathbf{r}-\mathbf{r}'|}}}\psi=\frac{1}{|\mathbf{r}-\mathbf{r}'|}為{\displaystyle\mathbf{r}'}\mathbf{r}'與{\displaystyle\mathbf{r}}\mathbf{r}之間的距離。應用泊松方程{\displaystyle\nabla^{2}\phi(\mathbf{r})=-\rho/\epsilon _{0}}\nabla^2\phi(\mathbf{r})=-\rho/\epsilon_0,則可得到
{\displaystyle\int _{\mathbb{V}'}\left[\phi(\mathbf{r}')\nabla^{2}\left({\frac{1}{|\mathbf{r}-\mathbf{r}'|}}\right)+{\frac{\rho(\mathbf{r}')}{\epsilon _{0}|\mathbf{r}-\mathbf{r}'|}}\right]\mathrmkmk00wm^{3}r'=\oint _{\mathbb{S}'}\left[\phi\{\partial\over\partial n'}\left({\frac{1}{|\mathbf{r}-\mathbf{r}'|}}\right)-\left({\frac{1}{|\mathbf{r}-\mathbf{r}'|}}\right){\partial\phi\over\partial n'}\right]\mathrmkmk00wm^{2}r'}\int_{\mathbb{V}'}\left[\phi(\mathbf{r}')\nabla^2\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right)+\frac{\rho(\mathbf{r}')}{\epsilon_0|\mathbf{r}-\mathbf{r}'|}\right]\mathrmkmk00wm^3 r'=\oint_{\mathbb{S}'}\left[\phi\{\partial\over\partial n'}\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right)-\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right){\partial\phi\over\partial n'}\right]\mathrmkmk00wm^2 r'。
再應用向量恒等式
{\displaystyle\nabla^{2}\left({\frac{1}{|\mathbf{r}-\mathbf{r}'|}}\right)=-4\pi\delta(\mathbf{r}-\mathbf{r}')}\nabla^2\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right)=-4\pi\delta(\mathbf{r}-\mathbf{r}')。
假設檢驗位置{\displaystyle\mathbf{r}}\mathbf{r}在積分體積{\displaystyle\mathbb{V}'}\mathbb{V}'內,則可得到
{\displaystyle\phi(\mathbf{r})={\frac{1}{4\pi\epsilon _{0}}}\int _{\mathbb{V}'}{\frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}}\\mathrmkmk00wm^{3}r'+{\frac{1}{4\pi}}\oint _{\mathbb{S}'}\left[\left({\frac{1}{|\mathbf{r}-\mathbf{r}'|}}\right){\partial\phi\over\partial n'}-\phi\{\partial\over\partial n'}\left({\frac{1}{|\mathbf{r}-\mathbf{r}'|}}\right)\right]\mathrmkmk00wm^{2}r'}\phi(\mathbf{r})=\frac{1}{4\pi\epsilon_0}\int_{\mathbb{V}'}\frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\\mathrmkmk00wm^3 r'+\frac{1}{4\pi}\oint_{\mathbb{S}'}\left[\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right){\partial\phi\over\partial n'}-\phi\{\partial\over\partial n'}\left(\frac{1}{|\mathbf{r}-\mathbf{r}'|}\right)\right]\mathrmkmk00wm^2 r'。
這方程右手邊的體積分就是電勢的方程(1),而面積分就是因為邊界條件而添加的項目。這是{\displaystyle\mathbb{V}'}\mathbb{V}'體內與體外之間的邊界曲面。面積分的第一個項目要求給定在邊界曲面的法向電場,即{\displaystyle E_{n'}=-{\partial\phi\over\partial n'}}E_{n'}=-{\partial\phi\over\partial n'},也就是面感應電荷密度{\displaystyle\sigma=\epsilon _{0}E_{n'}}\sigma=\epsilon_0 E_{n'}。面積分的第二個項目要求給定在邊界曲面的電勢{\displaystyle\phi}\phi。假若能夠知道積分體積內的電荷密度、在閉曲面的面電荷密度與電勢,就可以計算出在積分體積內任意位置的電勢。
根據柯西邊界條件,有時候,給定在邊界曲面的法向電場與電勢,可能會因為給定過多邊界條件,而造成無法計算出一致的電勢的狀況。實際而言,只要給定法向電場或電勢,兩者之一,就可以計算出電勢。[5]
假若積分體積為無窮大空間,當{\displaystyle r'}r'趨向于無窮大時,則面積分的被積分項目會以{\displaystyle 1/r'^{3}}1/r'^3速率遞減,而積分面積會以{\displaystyle r'^{2}}r'^2速率遞增,所以,面積分項目會趨向于零,這方程約化為先前的電勢方程(1)。
格林函數
包括函數{\displaystyle 1/|\mathbf{r}-\mathbf{r}'|}1/|\mathbf{r}-\mathbf{r}'|在內,有一類函數{\displaystyle G(\mathbf{r},\mathbf{r}')}G(\mathbf{r},\mathbf{r}'),稱為格林函數,能夠滿足方程
{\displaystyle\nabla^{2}G(\mathbf{r},\mathbf{r}')=-4\pi\delta(\mathbf{r}-\mathbf{r}')}\nabla^2 G(\mathbf{r},\mathbf{r}')=-4\pi\delta(\mathbf{r}-\mathbf{r}')。
另外,假設函數{\displaystyle H(\mathbf{r},\mathbf{r}')}H(\mathbf{r},\mathbf{r}')滿足拉普拉斯方程
{\displaystyle\nabla^{2}H(\mathbf{r},\mathbf{r}')=0}\nabla^2 H(\mathbf{r},\mathbf{r}')=0,
則函數{\displaystyle G'(\mathbf{r},\mathbf{r}')=G(\mathbf{r},\mathbf{r}')+H(\mathbf{r},\mathbf{r}')}G'(\mathbf{r},\mathbf{r}')=G(\mathbf{r},\mathbf{r}')+H(\mathbf{r},\mathbf{r}')也是格林函數。
應用這靈活性質,可以更嚴格地規定格林函數:[5]
對于狄利克雷問題,當源位置{\displaystyle\mathbf{r}'}\mathbf{r}'在邊界表面{\displaystyle{\mathbb{S}'}}{\mathbb{S}'}時,規定格林函數{\displaystyle G_{D}(\mathbf{r},\mathbf{r}')=0}G_D(\mathbf{r},\mathbf{r}')=0。這樣,從格林第二恒等式,設定{\displaystyle\phi(\mathbf{r}')}\phi(\mathbf{r}')為在{\displaystyle\mathbf{r}'}\mathbf{r}'的電勢,{\displaystyle\psi(\mathbf{r},\mathbf{r}')=G_{D}(\mathbf{r},\mathbf{r}')}\psi(\mathbf{r},\mathbf{r}')=G_D(\mathbf{r},\mathbf{r}'),則可得到
{\displaystyle\phi(\mathbf{r})={\frac{1}{4\pi\epsilon _{0}}}\int _{\mathbb{V}'}\rho(\mathbf{r}')G_{D}(\mathbf{r},\mathbf{r}')\\mathrmkmk00wm^{3}r'-\{\frac{1}{4\pi}}\oint _{\mathbb{S}'}\phi(\mathbf{r}')\{\partial G_{D}(\mathbf{r},\mathbf{r}')\over\partial n'}\mathrmkmk00wm^{2}r'}\phi(\mathbf{r})=\frac{1}{4\pi\epsilon_0}\int_{\mathbb{V}'}\rho(\mathbf{r}')G_D(\mathbf{r},\mathbf{r}')\\mathrmkmk00wm^3 r'
-\\frac{1}{4\pi}\oint_{\mathbb{S}'}\phi(\mathbf{r}')\{\partial G_D(\mathbf{r},\mathbf{r}')\over\partial n'}\mathrmkmk00wm^2 r'。(2)
對于滿足紐曼問題,當源位置{\displaystyle\mathbf{r}'}\mathbf{r}'在邊界表面{\displaystyle{\mathbb{S}'}}{\mathbb{S}'}時,規定格林函數{\displaystyle\oint _{\mathbb{S}'}{\frac{\partial G_{D}(\mathbf{r},\mathbf{r}')}{\partial n'}}\mathrmkmk00wm^{2}r'=-{\frac{4\pi}{S}}}\oint_{\mathbb{S}'}\frac{\partial G_D(\mathbf{r},\mathbf{r}')}{\partial n'}\mathrmkmk00wm^2 r'=-\frac{4\pi}{S}。
這兩種規定都能夠唯一地設定格林函數。注意到格林函數是一個幾何函數,與整個系統的電荷分布無關。對于任何系統,只要計算出適合其幾何形狀的格林函數,則不論系統的電荷分布為何,都可以使用同樣的格林函數。
無限平面導體案例
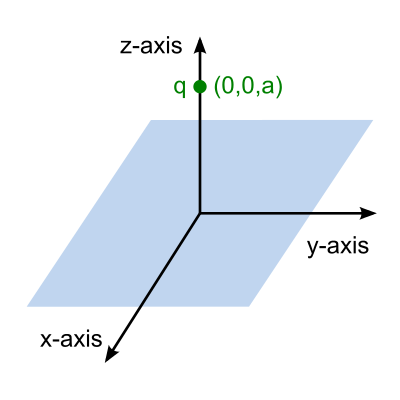
位于xy-平面的是一個接地的無限平面導體。其上方的點電荷{\displaystyle q}q的直角坐標是{\displaystyle(0,\,0,\,a)}(0,\,0,\,a)。
假設xy-平面是接地的無限平面導體,則對于z+半空間、滿足狄利克雷邊界條件的格林函數為
{\displaystyle{\begin{matrix}G_{D}(\mathbf{r},\mathbf{r}')={\cfrac{1}{\sqrt{(x-x')^{2}+(y-y')^{2}+(z-z')^{2}}}}\\\qquad\qquad\qquad-\{\cfrac{1}{\sqrt{(x-x')^{2}+(y-y')^{2}+(z+z')^{2}}}}\\\end{matrix}}}\begin{matrix}G_D(\mathbf{r},\mathbf{r}')=\cfrac{1}{\sqrt{(x-x')^2+(y-y')^2+(z-z')^2}}\\
\qquad\qquad\qquad-\\cfrac{1}{\sqrt{(x-x')^2+(y-y')^2+(z+z')^2}}\\
\end{matrix};
其中,{\displaystyle(x,y,z)}(x,y,z)、{\displaystyle(x',y',z')}(x',y',z')分別是檢驗位置{\displaystyle\mathbf{r}}\mathbf{r}、源位置{\displaystyle\mathbf{r}'}\mathbf{r}'的直角坐標。
由于接地導體的電勢為零,方程(2)的面積分項目等于零,方程(2)變為
{\displaystyle\phi(\mathbf{r})={\frac{1}{4\pi\epsilon _{0}}}\int _{\mathbb{V}'}\rho(\mathbf{r}')G_{D}(\mathbf{r},\mathbf{r}')\\mathrmkmk00wm^{3}r'}\phi(\mathbf{r})=\frac{1}{4\pi\epsilon_0}\int_{\mathbb{V}'}\rho(\mathbf{r}')G_D(\mathbf{r},\mathbf{r}')\\mathrmkmk00wm^3 r'
。
假設在位置{\displaystyle(0,0,a)}(0,0,a)有點電荷{\displaystyle q}q,則在z+半空間任意位置的電勢為
{\displaystyle{\begin{aligned}\phi(\mathbf{r})&={\frac{1}{4\pi\epsilon _{0}}}\int _{\mathbb{V}'}\rho(\mathbf{r}')\left({\frac{1}{\sqrt{x^{2}+y^{2}+(z-a)^{2}}}}-{\frac{1}{\sqrt{x^{2}+y^{2}+(z+a)^{2}}}}\right)\\mathrmkmk00wm^{3}r'\\&={\frac{1}{4\pi\epsilon _{0}}}\left({\frac{q}{\sqrt{x^{2}+y^{2}+(z-a)^{2}}}}-{\frac{q}{\sqrt{x^{2}+y^{2}+(z+a)^{2}}}}\right)\\\end{aligned}}}\begin{align}
\phi(\mathbf{r})&=\frac{1}{4\pi\epsilon_0}\int_{\mathbb{V}'}\rho(\mathbf{r}')\left(\frac{1}{\sqrt{x^2+y^2+(z-a)^2}}-\frac{1}{\sqrt{x^2+y^2+(z+a)^2}}\right)\\mathrmkmk00wm^3 r'\\
&=\frac{1}{4\pi\epsilon_0}\left(\frac{q}{\sqrt{x^2+y^2+(z-a)^2}}-\frac{q}{\sqrt{x^2+y^2+(z+a)^2}}\right)\\
\end{align}。
仔細檢察這方程,右手邊第一個項目,是在沒有平面導體的狀況時,點電荷{\displaystyle q}q所產生的電勢;右手邊第二個項目,是使用鏡像法時,鏡像電荷{\displaystyle-q}-q所產生的電勢。請參閱鏡像法條目的點電荷與無限平面導體段落。
導引
已知函數{\displaystyle 1/|\mathbf{r}-\mathbf{r}'|}1/|\mathbf{r}-\mathbf{r}'|為格林函數{\displaystyle G(\mathbf{r},\mathbf{r}')}G(\mathbf{r},\mathbf{r}'),滿足方程
{\displaystyle\nabla^{2}G(\mathbf{r},\mathbf{r}')=-4\pi\delta(\mathbf{r}-\mathbf{r}')}\nabla^2 G(\mathbf{r},\mathbf{r}')=-4\pi\delta(\mathbf{r}-\mathbf{r}')。
在三維無限空間里,{\displaystyle 1/|\mathbf{r}-\mathbf{r}'|}1/|\mathbf{r}-\mathbf{r}'|的傅里葉級數為[6]
{\displaystyle{\begin{aligned}{\frac{1}{|\mathbf{r}-\mathbf{r}'|}}&\equiv{\frac{1}{2\pi^{2}}}\int _{-\infty}^{\infty}\int _{-\infty}^{\infty}\int _{-\infty}^{\infty}\mathrmkmk00wm^{3}k{\frac{e^{i\mathbf{k}\cdot(\mathbf{r}-\mathbf{r}')}}{k^{2}}}\\&={\frac{1}{2\pi^{2}}}\int _{-\infty}^{\infty}\int _{-\infty}^{\infty}\mathrmkmk00wmk_{x}\\mathrmkmk00wmk_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty}^{\infty}\\mathrmkmk00wmk_{z}{\frac{e^{ik_{z}(z-z')}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}\\\end{aligned}}}\begin{align}\frac{1}{|\mathbf{r}-\mathbf{r}'|}
&\equiv\frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\mathrmkmk00wm^3 k\frac{e^{i\mathbf{k}\cdot(\mathbf{r}-\mathbf{r}')}}{k^2}\\
&=\frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\mathrmkmk00wmk_x\\mathrmkmk00wmk_y e^{ik_x(x-x')+ik_y(y-y')}\int_{-\infty}^{\infty}\\mathrmkmk00wmk_z\frac{e^{ik_z(z-z')}}{k_x^2+k_y^2+k_z^2}\\
\end{align}。
現在,必需找到格林函數{\displaystyle G_{D}(\mathbf{r},\mathbf{r}')=G(\mathbf{r},\mathbf{r}')+H(\mathbf{r},\mathbf{r}')}G_D(\mathbf{r},\mathbf{r}')=G(\mathbf{r},\mathbf{r}')+H(\mathbf{r},\mathbf{r}'),滿足狄利克雷邊界條件{\displaystyle G_{D}((x,y,0),\mathbf{r}')=0}G_D((x,y,0),\mathbf{r}')=0,同時,函數{\displaystyle H(\mathbf{r},\mathbf{r}')}H(\mathbf{r},\mathbf{r}')滿足拉普拉斯方程
{\displaystyle\nabla^{2}H(\mathbf{r},\mathbf{r}')=0}\nabla^2 H(\mathbf{r},\mathbf{r}')=0。
對于z+半空間,{\displaystyle H(\mathbf{r},\mathbf{r}')}H(\mathbf{r},\mathbf{r}')以傅里葉級數擴張為
{\displaystyle{\begin{aligned}H(\mathbf{r},\mathbf{r}')&={\frac{1}{2\pi^{2}}}\int _{-\infty}^{\infty}\int _{-\infty}^{\infty}\\mathrmkmk00wmk_{x}\\mathrmkmk00wmk_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty}^{\infty}\\mathrmkmk00wmk_{z}\left[B(\mathbf{k},z')e^{ik_{z}z}+C(\mathbf{k},z')e^{-ik_{z}z}\right]\\\end{aligned}}}\begin{align}H(\mathbf{r},\mathbf{r}')
&=\frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\\mathrmkmk00wmk_x\\mathrmkmk00wmk_y e^{ik_x(x-x')+ik_y(y-y')}\int_{-\infty}^{\infty}\\mathrmkmk00wmk_z\left[B(\mathbf{k},z')e^{ik_z z}+C(\mathbf{k},z')e^{-ik_z z}\right]\\
\end{align}。
對于x-坐標與對于y-坐標的傅里葉級數擴張,{\displaystyle H}H函數與{\displaystyle G}G函數的形式相同。這是因為對于無限空間案例與無限平面導體案例,兩種案例的x-邊界條件與y-邊界條件都相同,只有z-邊界條件稍有改變。將{\displaystyle H}H函數的方程代如,{\displaystyle G_{D}(\mathbf{r},\mathbf{r}')}G_D(\mathbf{r},\mathbf{r}')變為
{\displaystyle G_{D}(\mathbf{r},\mathbf{r}')={\frac{1}{2\pi^{2}}}\int _{-\infty}^{\infty}\int _{-\infty}^{\infty}\\mathrmkmk00wmk_{x}\\mathrmkmk00wmk_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty}^{\infty}\\mathrmkmk00wmk_{z}\left[{\frac{e^{ik_{z}(z-z')}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}+B(\mathbf{k},z')e^{ik_{z}z}+C(\mathbf{k},z')e^{-ik_{z}z}\right]}G_D(\mathbf{r},\mathbf{r}')
=\frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\\mathrmkmk00wmk_x\\mathrmkmk00wmk_y e^{ik_x(x-x')+ik_y(y-y')}\int_{-\infty}^{\infty}\\mathrmkmk00wmk_z\left[\frac{e^{ik_z(z-z')}}{k_x^2+k_y^2+k_z^2}+B(\mathbf{k},z')e^{ik_z z}+C(\mathbf{k},z')e^{-ik_z z}\right];
其中,{\displaystyle B(\mathbf{k},z')}B(\mathbf{k},z')與{\displaystyle C(\mathbf{k},z')}C(\mathbf{k},z')都是系數函數。
由于{\displaystyle G_{D}((x,y,0),\mathbf{r}')=0}G_D((x,y,0),\mathbf{r}')=0,對于任意{\displaystyle\mathbf{k}}\mathbf{k}與{\displaystyle z'}z',{\displaystyle B(\mathbf{k},z')}B(\mathbf{k},z')與{\displaystyle C(\mathbf{k},z')}C(\mathbf{k},z')之間的關系為
{\displaystyle{\frac{e^{-ik_{z}z'}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}+B(\mathbf{k},z')+C\mathbf{k},z')=0}\frac{e^{-ik_z z'}}{k_x^2+k_y^2+k_z^2}+B(\mathbf{k},z')+C\mathbf{k},z')=0、
{\displaystyle B(\mathbf{k},z')={\frac{B_{0}e^{-ik_{z}z'}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}}B(\mathbf{k},z')=\frac{B_0 e^{-ik_z z'}}{k_x^2+k_y^2+k_z^2}、
{\displaystyle C(\mathbf{k},z')={\frac{C_{0}e^{-ik_{z}z'}}{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}}C(\mathbf{k},z')=\frac{C_0 e^{-ik_z z'}}{k_x^2+k_y^2+k_z^2};
其中,{\displaystyle B_{0}}B_0與{\displaystyle C_{0}}C_{0}都是系數常數,而且,{\displaystyle B_{0}+C_{0}=-1}B_0+C_0=-1
將這些公式代入{\displaystyle G_{D}}G_D,可以得到
{\displaystyle G_{D}(\mathbf{r},\mathbf{r}')={\frac{1}{2\pi^{2}}}\int _{-\infty}^{\infty}\int _{-\infty}^{\infty}\\mathrmkmk00wmk_{x}\\mathrmkmk00wmk_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty}^{\infty}\\mathrmkmk00wmk_{z}\left\{{\frac{(1+B_{0})}{k^{2}}}\left[e^{ik_{z}(z-z')}-e^{ik_{z}(z+z')}\right]\right\}}G_D(\mathbf{r},\mathbf{r}')
=\frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\\mathrmkmk00wmk_x\\mathrmkmk00wmk_y e^{ik_x(x-x')+ik_y(y-y')}\int_{-\infty}^{\infty}\\mathrmkmk00wmk_z\left\{\frac{(1+B_0)}{k^2}\left[e^{ik_z(z-z')}-e^{ik_z(z+z')}\right]\right\}。
為了滿足方程{\displaystyle\nabla^{2}G_{D}(\mathbf{r},\mathbf{r}')=-4\pi\delta(\mathbf{r}-\mathbf{r}')}\nabla^2 G_D(\mathbf{r},\mathbf{r}')=-4\pi\delta(\mathbf{r}-\mathbf{r}'),必需設定{\displaystyle B_{0}=0}B_0=0。所以,
{\displaystyle{\begin{aligned}G_{D}(\mathbf{r},\mathbf{r}')&={\frac{1}{2\pi^{2}}}\int _{-\infty}^{\infty}\int _{-\infty}^{\infty}\\mathrmkmk00wmk_{x}\\mathrmkmk00wmk_{y}e^{ik_{x}(x-x')+ik_{y}(y-y')}\int _{-\infty}^{\infty}\\mathrmkmk00wmk_{z}\left\{{\frac{1}{k^{2}}}\left[e^{ik_{z}(z-z')}-e^{ik_{z}(z+z')}\right]\right\}\\&={\frac{1}{|\mathbf{r}-\mathbf{r}'|}}-{\frac{1}{|\mathbf{r}-\mathbf{r}''|}}\\&={\cfrac{1}{\sqrt{(x-x')^{2}+(y-y')^{2}+(z-z')^{2}}}}-\{\cfrac{1}{\sqrt{(x-x')^{2}+(y-y')^{2}+(z+z')^{2}}}}\\\end{aligned}}}\begin{align}G_D(\mathbf{r},\mathbf{r}')&=\frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\\mathrmkmk00wmk_x\\mathrmkmk00wmk_y e^{ik_x(x-x')+ik_y(y-y')}\int_{-\infty}^{\infty}\\mathrmkmk00wmk_z\left\{\frac{1}{k^2}\left[e^{ik_z(z-z')}-e^{ik_z(z+z')}\right]\right\}\\
&=\frac{1}{|\mathbf{r}-\mathbf{r}'|}-\frac{1}{|\mathbf{r}-\mathbf{r}''|}\\
&=\cfrac{1}{\sqrt{(x-x')^2+(y-y')^2+(z-z')^2}}-\\cfrac{1}{\sqrt{(x-x')^2+(y-y')^2+(z+z')^2}}\\
\end{align};
其中,{\displaystyle\mathbf{r}''=(x',y',-z')}\mathbf{r}''=(x',y',-z')是鏡像電荷的位置。
兩個半平面導體案例
假設在xy-平面的無限平面導體被一條位于{\displaystyle y=0}y=0的絕緣線條分為兩半,兩個處于y+、y--半平面的導體的電勢分別設定為{\displaystyle+V}+V與{\displaystyle-V}-V,則由于{\displaystyle\rho(\mathbf{r}')=0}\rho(\mathbf{r}')=0,方程(2)變為
{\displaystyle\phi(\mathbf{r})=-\{\frac{1}{4\pi}}\oint _{\mathbb{S}'}\phi(\mathbf{r}')\{\partial G_{D}(\mathbf{r},\mathbf{r}')\over\partial n'}\mathrmkmk00wm^{2}r'}\phi(\mathbf{r})=-\\frac{1}{4\pi}\oint_{\mathbb{S}'}\phi(\mathbf{r}')\{\partial G_D(\mathbf{r},\mathbf{r}')\over\partial n'}\mathrmkmk00wm^2 r'。(3)
注意到{\displaystyle\mathbb{V}'}\mathbb{V}'是z+-半空間,xy-平面是其邊界閉曲面的一部分,格林函數在xy-平面的法向導數的方向是朝著負z方向:
{\displaystyle{\begin{aligned}{\partial G_{D}\over\partial n'}&=-\{\partial G_{D}\over\partial z'}\\&=-\{\cfrac{z-z'}{[(x-x')^{2}+(y-y')^{2}+(z-z')^{2}]^{3/2}}}\-\{\cfrac{z+z'}{[(x-x')^{2}+(y-y')^{2}+(z+z')^{2}]^{3/2}}}\\&=-\{\cfrac{2z}{[(x-x')^{2}+(y-y')^{2}+z^{2}]^{3/2}}}\\\end{aligned}}}\begin{align}{\partial G_D\over\partial n'}&=-\{\partial G_D\over\partial z'}\\
&=-\\cfrac{z-z'}{[(x-x')^2+(y-y')^2+(z-z')^2]^{3/2}}\-\\cfrac{z+z'}{[(x-x')^2+(y-y')^2+(z+z')^2]^{3/2}}\\
&=-\\cfrac{2z}{[(x-x')^2+(y-y')^2+z^2]^{3/2}}\\
\end{align}。
{\displaystyle\mathbb{V}'}\mathbb{V}'的邊界閉曲面在無窮遠位置的電勢為0,所以,只需要計算xy-平面給出的貢獻,就可以得到在{\displaystyle\mathbb{V}'}\mathbb{V}'內部任意位置的電勢。將上述方程代入方程(3):[4]
{\displaystyle{\begin{aligned}\phi(\mathbf{r})&={\frac{2z}{4\pi}}\left\{\int _{0+}^{\infty}\int _{-\infty}^{\infty}{\cfrac{V\mathrmkmk00wmx'\mathrmkmk00wmy'}{[(x-x')^{2}+(y-y')^{2}+z^{2}]^{3/2}}}+\int _{-\infty}^{0-}\int _{-\infty}^{\infty}{\cfrac{-V\mathrmkmk00wmx'\mathrmkmk00wmy'}{[(x-x')^{2}+(y-y')^{2}+z^{2}]^{3/2}}}\right\}\\&=\{\frac{zV}{\pi}}\left\{\int _{0+}^{\infty}{\frac{\mathrmkmk00wmy'}{(y-y')^{2}+z^{2}}}-\int _{-\infty}^{0-}{\frac{\mathrmkmk00wmy'}{(y-y')^{2}+z^{2}}}\right\}\\&={\frac{2V}{\pi}}\\arctan{\left({\frac{y}{z}}\right)}\\\end{aligned}}}\begin{align}\phi(\mathbf{r})&=\frac{2z}{4\pi}\left\{\int_{0+}^{\infty}\int_{-\infty}^{\infty}\cfrac{V\mathrmkmk00wmx'\mathrmkmk00wmy'
}{[(x-x')^2+(y-y')^2+z^2]^{3/2}}+\int_{-\infty}^{0-}\int_{-\infty}^{\infty}\cfrac{-V\mathrmkmk00wmx'\mathrmkmk00wmy'
}{[(x-x')^2+(y-y')^2+z^2]^{3/2}}\right\}\\
&=\\frac{zV}{\pi}\left\{\int_{0+}^{\infty}\frac{\mathrmkmk00wmy'}{(y-y')^2+z^2}
-\int_{-\infty}^{0-}\frac{\mathrmkmk00wmy'}{(y-y')^2+z^2}\right\}\\
&=\frac{2V}{\pi}\\arctan{\left(\frac{y}{z}\right)}\\
\end{align}。
推廣至電動力學
假設磁場含時間(每當電場含時間,則此假設成立。逆過來亦成立),則不能簡單地以標勢{\displaystyle\phi}\phi描述電場。因為根據法拉第電磁感應定律,{\displaystyle\mathbf{\nabla}\times\mathbf{E}=-\{\frac{\partial\mathbf{B}}{\partial t}}\neq 0}\mathbf{\nabla}\times\mathbf{E}=-\\frac{\partial\mathbf{B}}{\partial t}\neq 0,電場不再具有保守性,{\displaystyle\int\mathbf{E}\cdot\mathrmkmk00wm{\boldsymbol{\ell}}}\int\mathbf{E}\cdot\mathrmkmk00wm\boldsymbol{\ell}跟路徑有關。
替代地,在定義標勢時,必須引入磁矢勢{\displaystyle\mathbf{A}}\mathbf{A},定義為
{\displaystyle\mathbf{B}\{\stackrel{def}{=}}\\mathbf{\nabla}\times\mathbf{A}}\mathbf{B}\\stackrel{def}{=}\\mathbf{\nabla}\times\mathbf{A};
其中,{\displaystyle\mathbf{B}}\mathbf{B}是磁場。
根據亥姆霍茲定理[7](Helmholtz theorem),假設一個向量函數{\displaystyle\mathbf{F}(\mathbf{r})}\mathbf{F}(\mathbf{r})滿足以下兩條件:
{\displaystyle\nabla\cdot\mathbf{F}(\mathbf{r})=D(\mathbf{r})}\nabla\cdot\mathbf{F}(\mathbf{r})=D(\mathbf{r})、
{\displaystyle\nabla\times\mathbf{F}(\mathbf{r})=\mathbf{C}(\mathbf{r})}\nabla\times\mathbf{F}(\mathbf{r})=\mathbf{C}(\mathbf{r});
其中,{\displaystyle D(\mathbf{r})}D(\mathbf{r})是個標量函數,{\displaystyle\mathbf{C}(\mathbf{r})}\mathbf{C}(\mathbf{r})是個向量函數。
再假設{\displaystyle D(\mathbf{r})}D(\mathbf{r})和{\displaystyle\mathbf{C}(\mathbf{r})}\mathbf{C}(\mathbf{r}),在無窮遠處都足夠快速地趨向0,則{\displaystyle\mathbf{F}(\mathbf{r})}\mathbf{F}(\mathbf{r})可以用方程表達為
{\displaystyle\mathbf{F}(\mathbf{r})=-\nabla\left({\frac{1}{4\pi}}\int _{\mathbb{V}'}{\frac{D(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}}\mathrmkmk00wm^{3}r'\right)+\nabla\times\left({\frac{1}{4\pi}}\int _{\mathbb{V}'}{\frac{\mathbf{C}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}}\mathrmkmk00wm^{3}r'\right)}\mathbf{F}(\mathbf{r})=-\nabla\left(\frac{1}{4\pi}\int_{\mathbb{V}'}\frac{D(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrmkmk00wm^3 r'\right)+\nabla\times\left(\frac{1}{4\pi}\int_{\mathbb{V}'}\frac{\mathbf{C}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrmkmk00wm^3 r'\right);
在這里,{\displaystyle\nabla}\nabla只作用于{\displaystyle\mathbf{r}}\mathbf{r},體積分的體積為{\displaystyle\mathbb{V}'}\mathbb{V}'。
采用庫侖規范(Coulomb gauge),則磁矢勢{\displaystyle\mathbf{A}}\mathbf{A}遵守
{\displaystyle\mathbf{\nabla}\cdot\mathbf{A}=0}\mathbf{\nabla}\cdot\mathbf{A}=0。
所以,
{\displaystyle\mathbf{A}(\mathbf{r})=\nabla\times\left({\frac{1}{4\pi}}\int _{\mathbb{V}'}{\frac{\mathbf{B}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}}\mathrmkmk00wm^{3}r'\right)={\frac{1}{4\pi}}\int _{\mathbb{V}'}\mathbf{B}(\mathbf{r}')\times{\frac{\mathbf{r}-\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|^{3}}}\mathrmkmk00wm^{3}r'}\mathbf{A}(\mathbf{r})=\nabla\times\left(\frac{1}{4\pi}\int_{\mathbb{V}'}\frac{\mathbf{B}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrmkmk00wm^3 r'\right)=\frac{1}{4\pi}\int_{\mathbb{V}'}\mathbf{B}(\mathbf{r}')\times\frac{\mathbf{r}-\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|^3}\mathrmkmk00wm^3 r'。
注意到,以上這些推導,并沒有涉及時間參數。加入時間參數{\displaystyle t}t,結果也成立。所以,永遠可以找到磁矢勢{\displaystyle\mathbf{A}}\mathbf{A}:
{\displaystyle\mathbf{A}(\mathbf{r},\,t)={\frac{1}{4\pi}}\int _{\mathbb{V}'}\mathbf{B}(\mathbf{r}',\,t)\times{\frac{\mathbf{r}-\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|^{3}}}\mathrmkmk00wm^{3}r'}\mathbf{A}(\mathbf{r},\,t)=\frac{1}{4\pi}\int_{\mathbb{V}'}\mathbf{B}(\mathbf{r}',\,t)\times\frac{\mathbf{r}-\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|^3}\mathrmkmk00wm^3 r'。
根據法拉第電磁感應定律,向量場{\displaystyle\mathbf{G}=\mathbf{E}+\partial\mathbf{A}/\partial t}\mathbf{G}=\mathbf{E}+\partial\mathbf{A}/\partial t是一個保守場:
{\displaystyle\nabla\times\mathbf{G}=\nabla\times\mathbf{E}+\nabla\times\partial\mathbf{A}/\partial t=0}\nabla\times\mathbf{G}=\nabla\times\mathbf{E}+\nabla\times\partial\mathbf{A}/\partial t=0。
所以,必定可以找到標勢{\displaystyle\phi}\phi,滿足{\displaystyle\mathbf{G}=-\nabla\phi}\mathbf{G}=-\nabla\phi。因此,下述方程成立:
{\displaystyle\mathbf{E}=-\mathbf{\nabla}\phi-{\frac{\partial\mathbf{A}}{\partial t}}}\mathbf{E}=-\mathbf{\nabla}\phi-\frac{\partial\mathbf{A}}{\partial t}。
靜電勢只是這含時定義的一個特別案例,在這案例里,磁矢勢{\displaystyle\mathbf{A}}\mathbf{A}不含時間。從另一方面來說,對于含時向量場,電場的路徑積分與靜電學的結果大不相同:
{\displaystyle\int _{a}^{b}\mathbf{E}\cdot\mathrmkmk00wm{\boldsymbol{\ell}}\neq\phi(b)-\phi(a)}\int_a^b\mathbf{E}\cdot\mathrmkmk00wm\boldsymbol{\ell}\neq\phi(b)-\phi(a)。
關于電勢,小編為大家就分享這些。歡迎聯系我們合運電氣有限公司,以獲取更多相關知識。










 魯公網安備 37010502001687號
魯公網安備 37010502001687號


